OESJECTIFS
n Présenter la cinématique.
w Définir les notions de solide ou repère de référence, de mouvements absolu et relatif.
n Introduire les principaux mouvements de solides, la notion de points coïncidents et de trajectoire.
n Définir les principales grandeurs cinématiques : vecteur-position, vecteur-déplacement, vitesse et accélération d’un point.
n Fournir des éléments concernant le repérage des solides.
La cinématique est la partie de la mécanique qui étudie le mouvement des corps, indépendamment des forces qui les produisent. Les grandeurs étudiées s’appellent mouvement, déplacement, trajectoire, vitesse et accélération. Le mot cinématique dérive du grec kinema, qui signifie mouvement.
La cinématique présente deux types d’applications. La première voie est orientée vers l’analyse des grandeurs cinématiques liées aux mécanismes et aux machines. Son but est de définir la géométrie’ et les dimensions des pièces ou composants, tout en remarquant que la géométrie retenue a une influence sur les efforts engendrés. Exemples : engrenages, transmissions diverses, cames, etc. La deuxième voie est celle de la dynamique et
de l’énergétique qui, pour déterminer les mouvements à partir des efforts qui les pro- i duisent, fait largement appel aux grandeurs de la cinématique.
Remarque : en cinématique, les solides étudiés sont supposés indéformables. Un solide peut être défini comme un ensemble de points dont les distances respectives restent inchangées au cours du temps.
1 - Solide ou repère de référence - Référentiel
1. Repère et solide de référence
En cinématique, le mouvement d’un solide peut être défini par rapport à un autre solide choisi comme référence et appelé solide de référence.
Un repère de référence est un repère d’espace (exemples : repères cartésiens (0 ; x, y] ou (0 ; x, y, z)) lié ou “collé” au solide de référence, permettant de repérer avec précision la position et le mouvement du solide.
Exemple
Si l’on considère le mouvement de l’avion (1) par rapport au sol (0), noté Mtil,,,, le sol est le solide de référence.
Un observateur, immobile au sol, voyant l’avion évoluer dans le ciel, peut servir d’origine à un repère de référence lié à (0). Mti,,, définit le mouvement inverse,
l’avion est le solide de référence. Le pilote, immobile dans l’appareil, voit le sol défiler sous ses yeux et peut servir d’origine à un repère de référence lié à (1).
2. Repère de temps
Schématisation du temps
En mécanique classique, le temps est’ considéré comme absolu et uniforme. Chaque moment, chaque fragment de temps est identique au suivant.
Le temps peut être schématisé par une droite, orientée du passé vers l’avenir, avec au besoin une origine des temps (t = 0). L’image équivalente de cet espace est une montre ou un chronomètre. La lettre t, appelée date, symbolise un point de cet espace.
Unité : la seconde, symbole s, est l’unité de base légale (unité SI) du temps.
Les autres unités usuelles sont également utilisables : minute, heure, jour, année, etc.
Remarque : quelques notions concernant la relativité du temps sont proposées au chapitre (( dynamique - mouvements plans ».
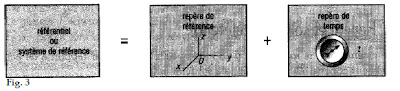
3. Système de référence ou référentiel
Un système de référence est l’addition ou la combinaison d’un repère de référence et d’un repère de temps.
Remarque : en cinématique, le mouvement des solides sera défini par rapport à un système de référence.
II - Mouvements absolu et relatif
10. Généralités - trajectoires
1, Mouvement absolu
Le mouvement d’un solide est dit absolu s’il est défini ou décrit par rapport à un référentiel absolu.
Un référentiel absolu (ou galiléen) est un référentiel au repos absolu dans l’univers.
En mécanique industrielle, la Terre peut être assimilée, avec une très bonne approximation, à un référentiel absolu (voir le chapitre « dynamique - mouvements plans j)).
Remarque : à la notion de mouvement absolu correspond les notions de vitesses absolues et d’accélérations absolues.
2, Mouvement relatif10. Généralités - trajectoires
1, Mouvement absolu
Le mouvement d’un solide est dit absolu s’il est défini ou décrit par rapport à un référentiel absolu.
Un référentiel absolu (ou galiléen) est un référentiel au repos absolu dans l’univers.
En mécanique industrielle, la Terre peut être assimilée, avec une très bonne approximation, à un référentiel absolu (voir le chapitre « dynamique - mouvements plans j)).
Remarque : à la notion de mouvement absolu correspond les notions de vitesses absolues et d’accélérations absolues.
Le mouvement d’un k&le est dît relatif s’il est défini par rappmt A un référentiel relatif.
Un reférentiel en mouvement dans l’univers est un réferentiel relatif.
À la notion de mouvement relatif correspond les notions de vitesses relatives et d’accélérations relatives.
Exemple : prenons le cas d’un voyageur (2) marchant dans un wagon (1) en mouvement par rapport au sol (0).
R, = (0, x0, y,), lié à la terre, est un repère absolu.
R, = (A, x1, yr), lié au wagon et R, (G, x2, yi>) lié au voyageur sont des repères relatifs.
Les mouvements Mti2,0 et Mtil,o sont des mouvements absolus. WA est un mouvement relatif ;. même chose pour son mouvement inverse MtiI,2.
Remarque : le mouvement Mti2,0 résulte de la combinaison des deux mouvements M% et M%-
R, = (A, x1, yr), lié au wagon et R, (G, x2, yi>) lié au voyageur sont des repères relatifs.
Les mouvements Mti2,0 et Mtil,o sont des mouvements absolus. WA est un mouvement relatif ;. même chose pour son mouvement inverse MtiI,2.
Remarque : le mouvement Mti2,0 résulte de la combinaison des deux mouvements M% et M%-
III - Principaux mouvements plans de solides
Un solide exécute un mouvement plan lorsque tous les points qui le constitue se déplacent dans des plans parallèles entre eux. Par commodité, le plan retenu pour définir le mouvement sera celui qui contient le centre de gravité G et le solide sera assimilé à une fine feuille ou à une fine lamelle. Cette schématisation permet de rassembler dans une même catégorie la plupart des mouvements de solides rencontrés en technologie : translations, rotations et mouvements plans généraux.
Un solide exécute un mouvement plan lorsque tous les points qui le constitue se déplacent dans des plans parallèles entre eux. Par commodité, le plan retenu pour définir le mouvement sera celui qui contient le centre de gravité G et le solide sera assimilé à une fine feuille ou à une fine lamelle. Cette schématisation permet de rassembler dans une même catégorie la plupart des mouvements de solides rencontrés en technologie : translations, rotations et mouvements plans généraux.
Un solide se déplace en translation si n’importe quelle ligne (AB) de celui-ci reste constamment parallèle à sa position initiale au cours du mouvement. À tout instant, il n’y a aucune rotation de AB.
Remarque : dans l’espace, deux lignes non parallèles seront nécessaires pour définir une translation.
Translation rectiligbe : tous les points du solide se déplacent suivant des lignes parallèles entre elles.
Translation curviligne : les points du solide se déplacent suivant des courbes géométriques identiques ou superposables.
2, Rotation (autour d’un axe fixe)
Le solide tourne ou est animé d’un mouvement angulaire autour d’un axe fixe perpendiculaire au plan du mouvement.
Les points du solide décrivent des cercles ou des circonférences centrés sur l’axe.
Toutes les lignes ou droites du solide tournent du même angle 19 à chaque instant considéré.
3. Mouvement plan général
Un mouvement plan général n’est ni une translation, ni une rotation. Tous les points du solide se déplacent dans des plans parallèles entre eux aux cours du mouvement.
Remarque : un mouvement plan peut être considéré comme la combinaison d’une translation et d’une rotation.
Exemple : flèche de pelle hydraulique. On suppose que les trois vérins hydrauliques
(10 + 1 l), (8 + 9) et (6 + 7) sont alimentés.
M%l = rotation de centre B ; Mti2,1 = rotation de centre F ;
Fd2 = rotation de centre M ; Mti3,2 = rotation de centre L ;
Ma rl,rO = translation rectiligne de direction AC ;
KV3 = translation rectiligne de direction DE ;
W,6 = translation rectiligne de direction KP.
Les mouvements suivants sont tous des mouvements plans généraux :
M”& ; MtisjO ; M”& ; Mti3,0 ; Mtill,o ; M”& ; M%,, ; M”& ; M&, etc.
IV - Points coïncidents et trajectoire
1, Notion de points coïncidents

Les solides (1) et (2) sont en mouvement entre eux et en mouvement par rapport au solide de référence (0). À un instant t quelconque, le point géométrique M peut être considéré comme lié, ou appartenant, à l’un quelconque des trois solides (0, 1 ou 2) et suivre le mouvement du solide auquel il est lié.
Trois cas possibles : M lié à 1 (M,), M lié à 2 (M,) et M lié à 0 (A&).
Les points M,, M, et Mo sont par définition des points coïncidents à l’instant t.
Remarque 1 : il n’est pas nécessaire que M soit un point matériel du solide auquel il est lié (c’est le cas de M, et MJ.
À partir de la notion de points coïncidents, il est plus facile de différencier les grandeurs cinématiques (trajectoires, vitesses, etc.) des points de chacun des solides.
Par exemple,. pour le mzment MtiI,o au point M, on peut définir TIM1,0 (la trajectoire), V,,,, (la vitesse) et aM1,0 (l’accélération) du point M, lié à 1 par rapport à 0 ou R,.
Même remarque pour les mouvements Mti2,0 et Mti2,r.
Remarque 2 : il peut arriver que les points M,, M2 et M, coïncident à tous les instants, on dit alors qu’ils sont constamment en coïncidence.
Exemple : ensemble des points appartenant à l’axe de rotation d’un solide.
Trois cas possibles : M lié à 1 (M,), M lié à 2 (M,) et M lié à 0 (A&).
Les points M,, M, et Mo sont par définition des points coïncidents à l’instant t.
Remarque 1 : il n’est pas nécessaire que M soit un point matériel du solide auquel il est lié (c’est le cas de M, et MJ.
À partir de la notion de points coïncidents, il est plus facile de différencier les grandeurs cinématiques (trajectoires, vitesses, etc.) des points de chacun des solides.
Par exemple,. pour le mzment MtiI,o au point M, on peut définir TIM1,0 (la trajectoire), V,,,, (la vitesse) et aM1,0 (l’accélération) du point M, lié à 1 par rapport à 0 ou R,.
Même remarque pour les mouvements Mti2,0 et Mti2,r.
Remarque 2 : il peut arriver que les points M,, M2 et M, coïncident à tous les instants, on dit alors qu’ils sont constamment en coïncidence.
Exemple : ensemble des points appartenant à l’axe de rotation d’un solide.
2. Trajectoire d’un point
La trajectoire du point M est la courbe géométrique décrite au cours du temps par les positions successives de celui-ci dans le repère de référence R,.
Remarque : si M appartient à un solide (l), la trajectoire de M, notée TMl,,,, est définie par l’ensemble des points Mo qui coïncident avec M, au cours du temps.
La trajectoire du point M est la courbe géométrique décrite au cours du temps par les positions successives de celui-ci dans le repère de référence R,.
Remarque : si M appartient à un solide (l), la trajectoire de M, notée TMl,,,, est définie par l’ensemble des points Mo qui coïncident avec M, au cours du temps.
Exemple : roue avant de bicyclette.
A est le point decontact entre la I TLZO I lC’ roue (1) et le sol (0). B est le centre de l’articulation (ou dumoyeu) entre la roue (1) et le cadre (2). C est un A A' point appartenant Fig. ’ à une poignée de frein. Le vélo se déplace en translation rectiligne. Pour un tour de roue : l Tc2,o = segment CC’, TB2,0 = segment BB’, TA2,0 = segment AA’ (TA2,0 c’est aussi la trace laissée par le pneu sur le sol). . L/2 est réduite au point B. B, et B, sont constamment en coïncidence. Il en résulte que G2,o est identique à TB1,O.
. T41/2 = cercle de centre B et de rayon AB. l L,o est une courbe particulière appelée cycloïde (voir figure).
V - Vecteur-position et vecteur-déplacement
La notion de vecteur-position est également abordée dans le chapitre “Vecteurs”.

















Aucun commentaire:
Enregistrer un commentaire